Optical properties
本文总结了一些研究发光或者光吸收材料的常用知识
- 荧光:激发态电子跃迁到低能态(通常为基态)发射的光子,发射过程对应初态和末态自旋重度(通常基态为单重态,此时激发态也为单重态)不发生变化,即为“偶极允许”跃迁过程,寿命短
- 磷光:发射过程初态和末态自旋重度发生变化(通常基态为单重态,磷光过程对应激发态为三重态),因此为“偶极禁止”跃迁过程,寿命长,在激发过程结束后,仍能发光。
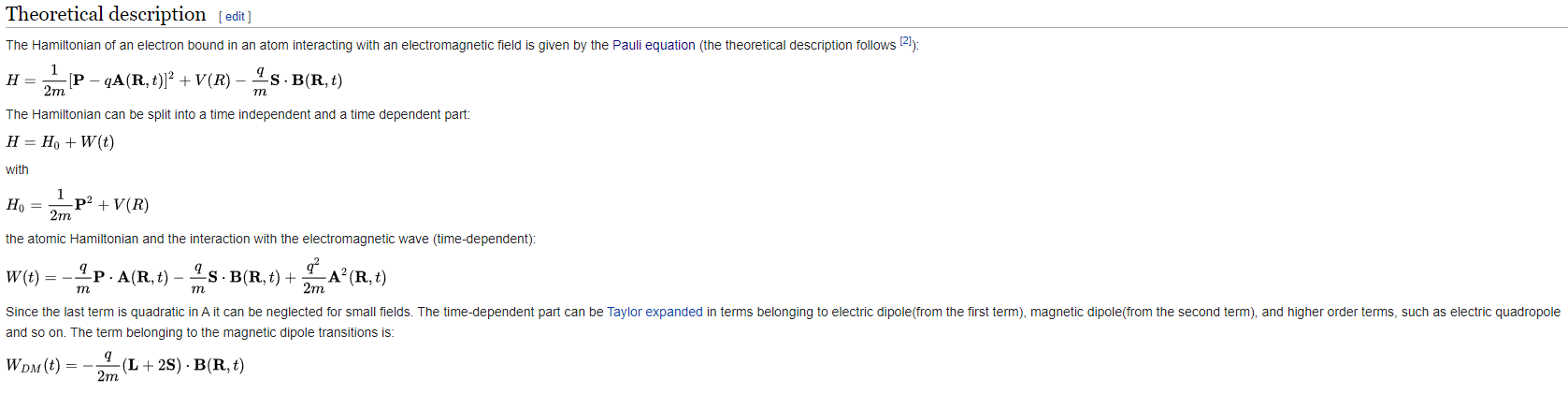
电偶极跃迁 - 从宇称角度考虑,电偶极矩算符(

磁偶极跃迁
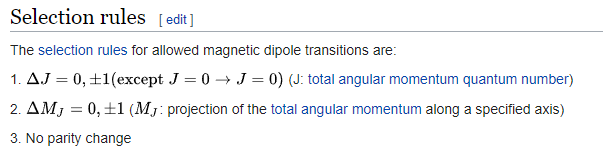
- 磁偶极算符和电四极矩算符是偶宇称的,连接两个宇称相同的态
- 磁偶极和电四极矩跃迁要弱于电偶极矩跃迁
- 原子核分子的电子态通常不一定有静态的电偶极矩额,但许多态会有静态的磁偶极矩
- 发射光谱:固定激发波的波长,测定发射光强度与波长(有时候也测波数或者频率等)的关系,通俗而不太严谨的说,发射光谱测定的是发射光的颜色。
- 激发光谱:固定发射光的波长,测量激发光的波长与荧光强度之间的关系。如从发射光谱知道某分子最大发射波长是500nm,我们希望知道用哪个波长的激发光照射这个分子,可以获得最大的发射强度,就可以通过测定激发光谱来实现。激发光谱通常形状与吸收谱类似,但性质不完全一样,因为激发光谱仅描述荧光跃迁能量,而吸收光谱不仅包含荧光跃迁部分能量,还包含如电子弛豫,散射等其他形式能量吸收。
- Stokes shift:发射(荧光和拉曼)光谱较相应的吸收光谱红移(即长波方向移动),即最大荧光波长和最大吸收波长之间的差。源于电子激发到激发态之后,激发态结构发生变化,而且由于电子-声子相互作用,缺陷结构的结构变化更大(Huang-Rhys理论),理论上通过垂直发射能和垂直吸收能模拟发射和吸收能量,前者通常小于后者,因此发射波长比吸收波长更长,即发射光子能量小于吸收光子,过程中发射声子。
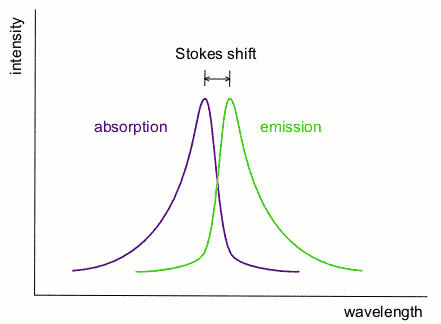
- anti-Stokes shift:发射(荧光和拉曼)光谱发生向短波方向的位移。即发射光子的能量大于吸收光子能量,说明过程中吸收声子。
- 绝热吸收:由零声子线(ZPL)描述,即过程中无声子参与
Coordination Configuration(CC) model
CC模型通常采用Franck-Condon(F-C)近似,即跃迁偶极仅考虑电子贡献,不考虑核坐标。绝热近似下,
Huang-Rhys factor
由于缺陷的存在,在电-声耦合相互作用下导致激发态原子构型和基态原子构型并不相同,电-声耦合作用通常会使电子(耦合系统)的能量降低,末态与初态构型的相对晶格位移(
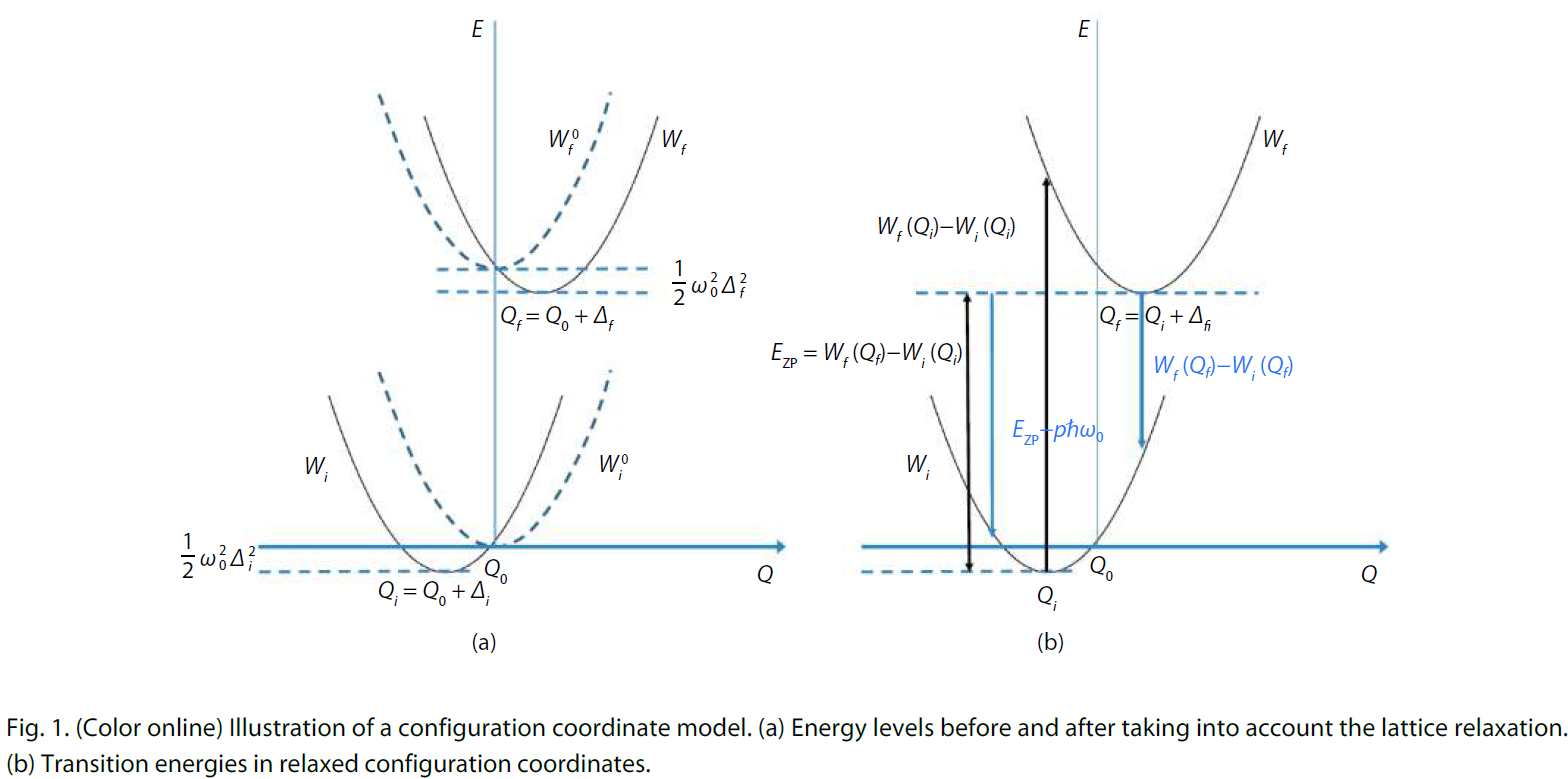 上图中
上图中
在Huang-Rhys理论中,对电-声相互作用哈密顿量和电子-电磁波相互作用哈密顿量采用了一阶微扰近似,电子系统能量和电偶极跃迁矩阵元中波函数采用零级波函数(仅有电子坐标,需要注意的是跃迁矩阵要乘以一个初态和末态振动波函数的内积,由于晶格弛豫,该内积不为1),此时光学跃迁相关的两个耦合态近似为
Albrecht理论则进一步采用了二阶微扰近似,此时跃迁矩阵包含电子态和振动态的混合,可以描述拉曼散射过程 -> 拉曼光谱
Raman effect
- 多数光子被大于自己直径的粒子散射后,出来的光子与入射前的能量相同,即发生弹性散射,称作瑞利散射;
- 少数光子被散射时发生非弹性散射,即散射前后光子能量发生变化,称作拉曼散射;拉曼散射根据光子能量变化分为两类
- Stokes散射:材料吸收能量,导致散射光子能量低于入射光子,为多数情况
- non-Stokes散射:材料失去能量,导致散射光子能量高于入射光子,为少数情况
Normalized luminescence intensity (line shape)
对于偶极允许跃迁(电偶极跃迁),
Frank-Condon近似下的归一化谱函数:
该式对所有能量为
评估谱函数的难点:
- 对所有相关振动自由度求和
- 激发态和基态振动模式通常不同,正则模式
(Duschinsky transformation),因此 是多维积分 ***
1D configuration coordinate diagram
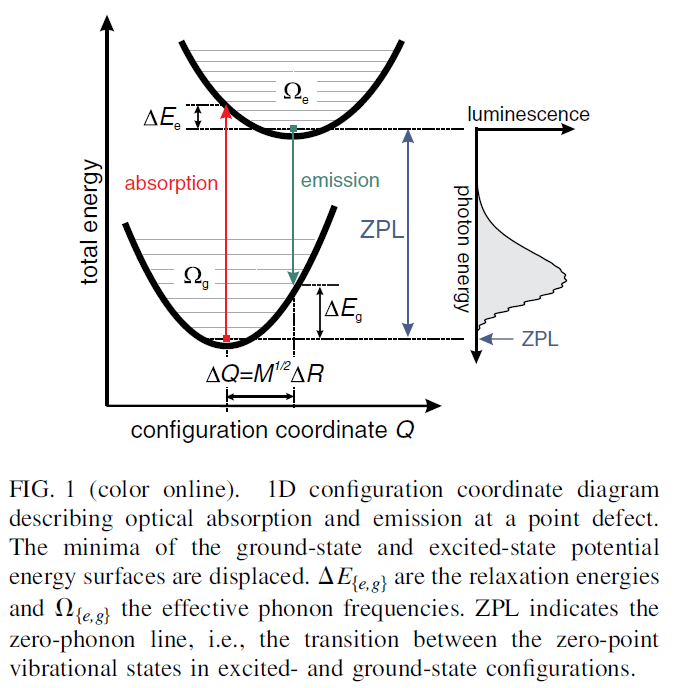
这里假设不同频率振动模式对于line shape的贡献可以被一个有效模式替代。1D模型包含的参数:有效振动的模型质量