白钨矿580nm波长的光,极大限制了其在量子信息领域的进一步应用。目前已有的解决方法是在 580nm波长的光,如何进一步提高光强,还有待进一步研究。
Introduction
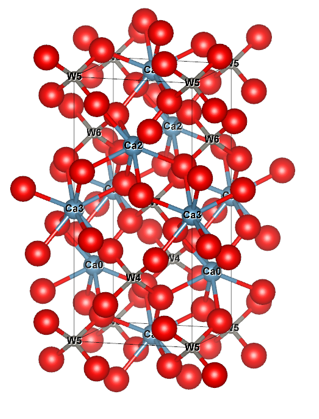
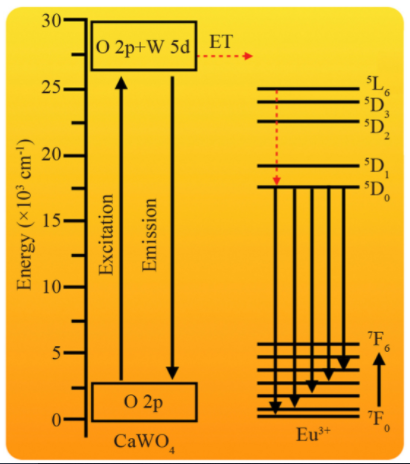
白钨矿
https://doi.org/10.1103/PhysRevB.57.12738 。下表给出一些典型白钨矿材料的光学参数:
对于掺杂三价镧系阳离子而言,能级跃迁通常会受到周围晶体场的影响,因此改变对称性会极大改变材料的发光性质。其中,https://doi.org/10.1021/acs.inorgchem.1c02450
Electronic configuration
电子排斥作用 :4f壳层电子之间的相互作用,自旋-轨道耦合 :电子绕核移动形成的磁场与电子自旋磁矩相互作导致晶体场微扰 :4f电子与配体中电子相互作用,打破了Zeeman效应 :对于较高的对称性,考虑外磁场作用下打破能级兼并,
Hund's rules 1. The spin multiplicity of the ground state has to be as large as possible; 2. In case there is more than one term with the same spin multiplicity, the term with the highest total orbital angular momentum(or L value) is the ground state; 3. For electronic shells that are less than half-filled, the ground state has the lowest possible J value. For electronic shells that are more than half-filled, the ground state has the highest possible J value. ***
根据Hund规则可以确立基态能级及其排列顺序,而激发态能级只能通过计算得到
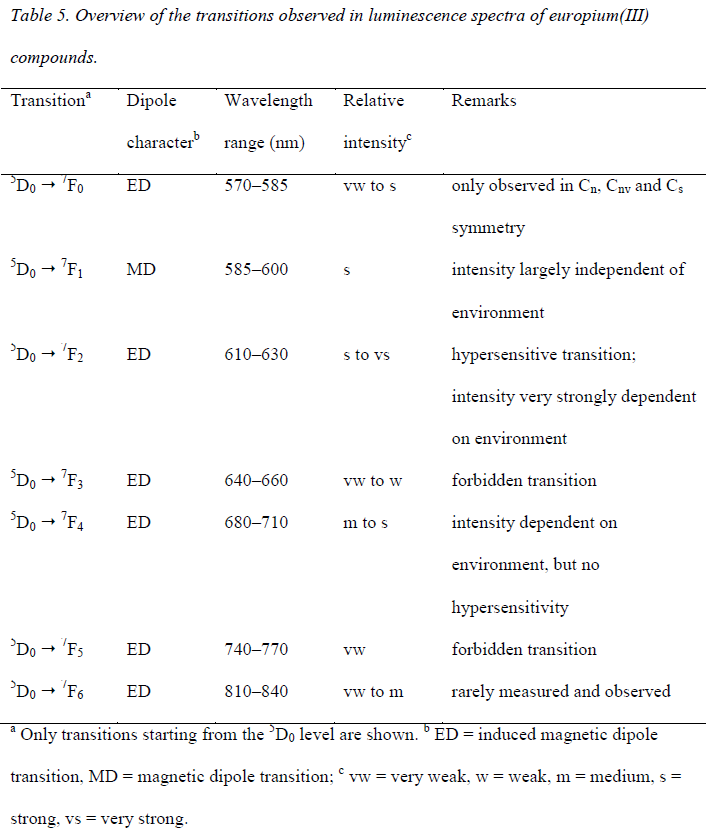
Luminescence spectra
induced电偶极跃迁源于晶体场效应打破了禁阻跃迁规则(Laporte selection rule:相同角量子数之间的电子跃迁是禁阻的,s->s,p->p,d->d,f->f是禁阻的),其强度相较于原始的电偶极跃迁更弱,通常利用Judd-Ofelt theory进行描述。而磁偶极跃迁是跃迁允许的,但是强度比induced电偶极跃迁要弱。在镧系光谱中并没有观察到电四极矩跃迁
Note: - 电偶极矩:电荷的线性位移,奇宇称 - 磁偶极矩:电荷的旋转位移,偶宇称 - 电四极矩:两个偶极排列使得整体的电荷和偶极矩为零,偶宇称 ***
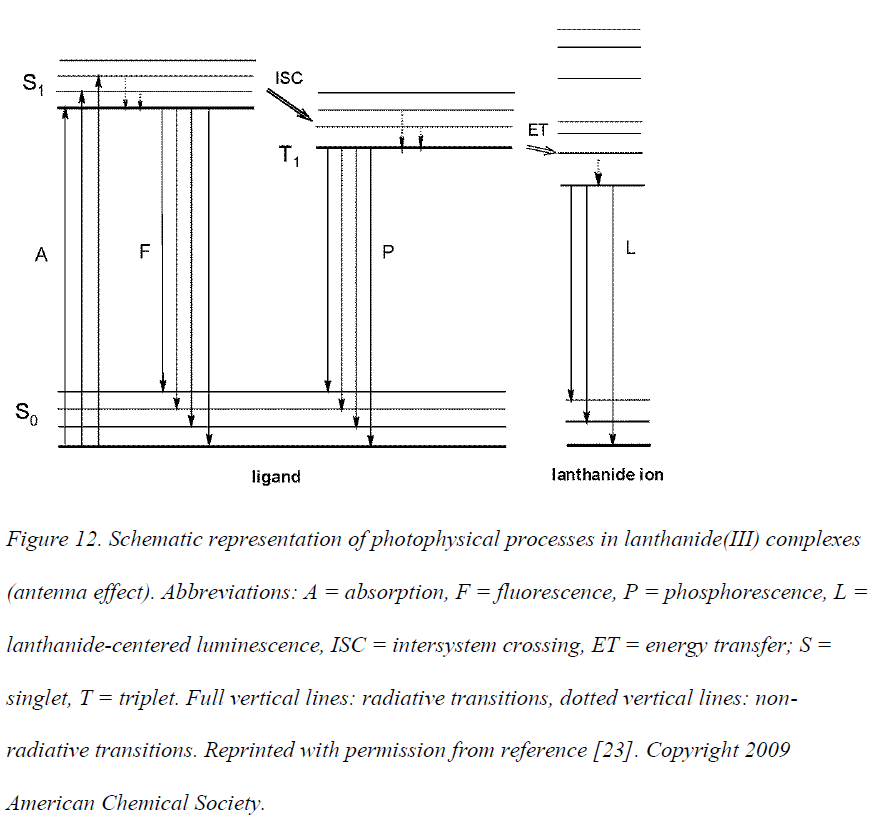
单重态的寿命较短,通常发生的是三重态到
Fig 1
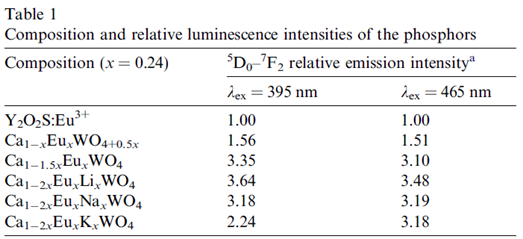
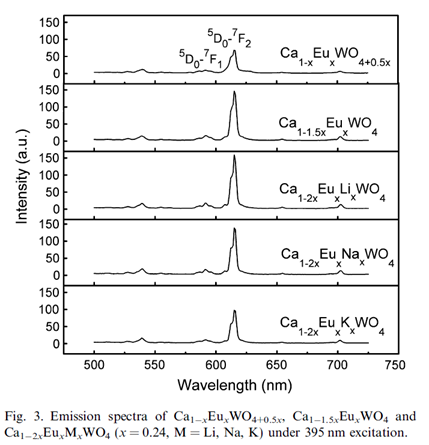
上图给出https://doi.org/10.1016/j.optmat.2007.10.007 。
Method
电荷补偿
选取不同的电荷补偿方式对于发光强度有影响,特别是https://doi.org/10.1016/j.optmat.2007.10.007 。
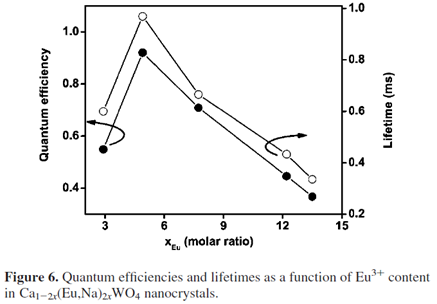
掺杂浓度
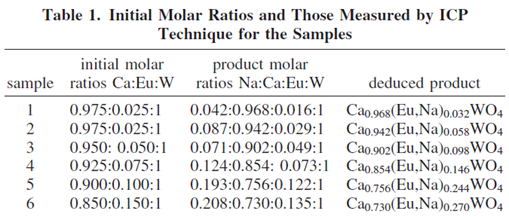
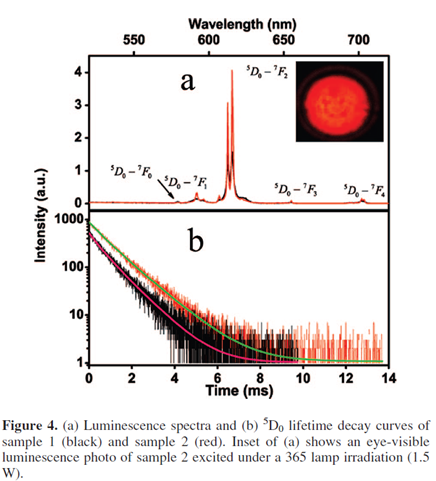
对于https://doi.org/10.1021/cm8014435 。
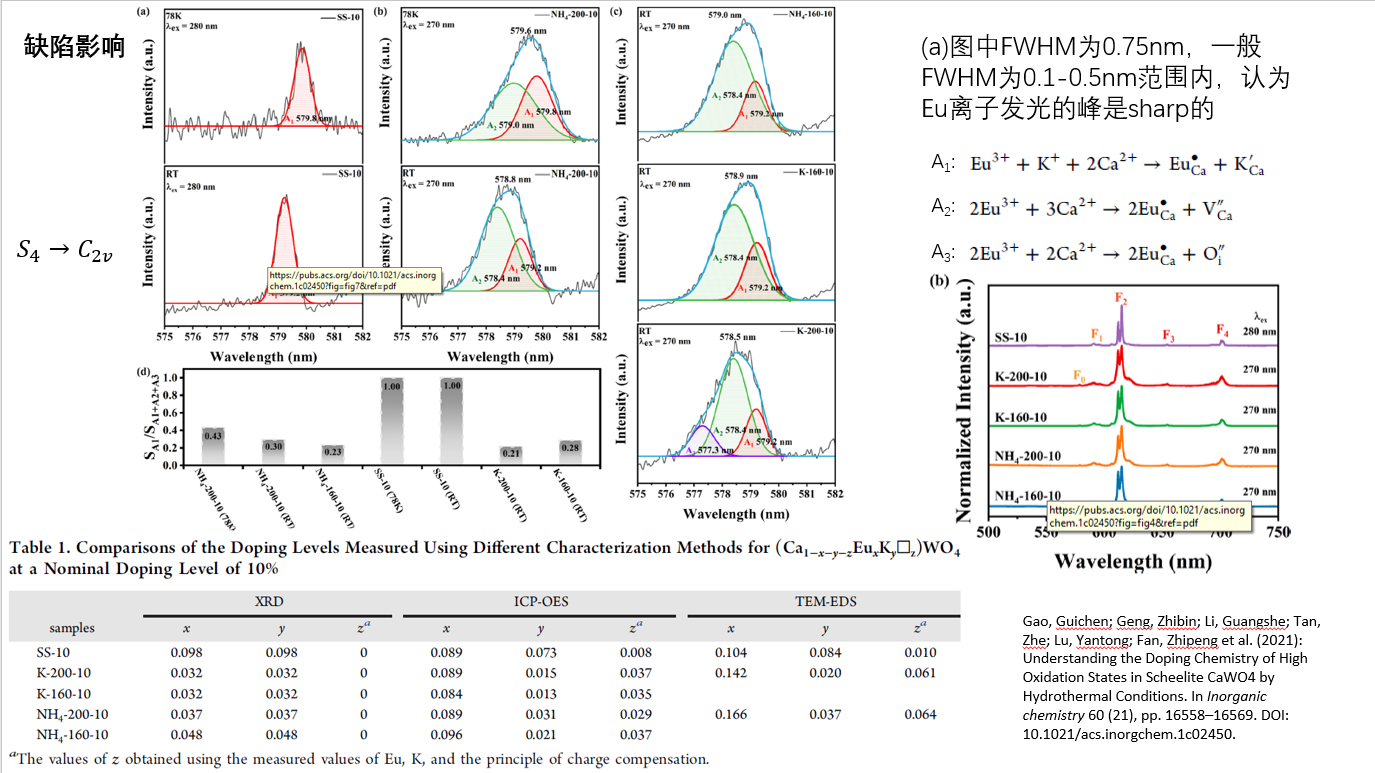
缺陷影响
K替位后Eu site的对称性由
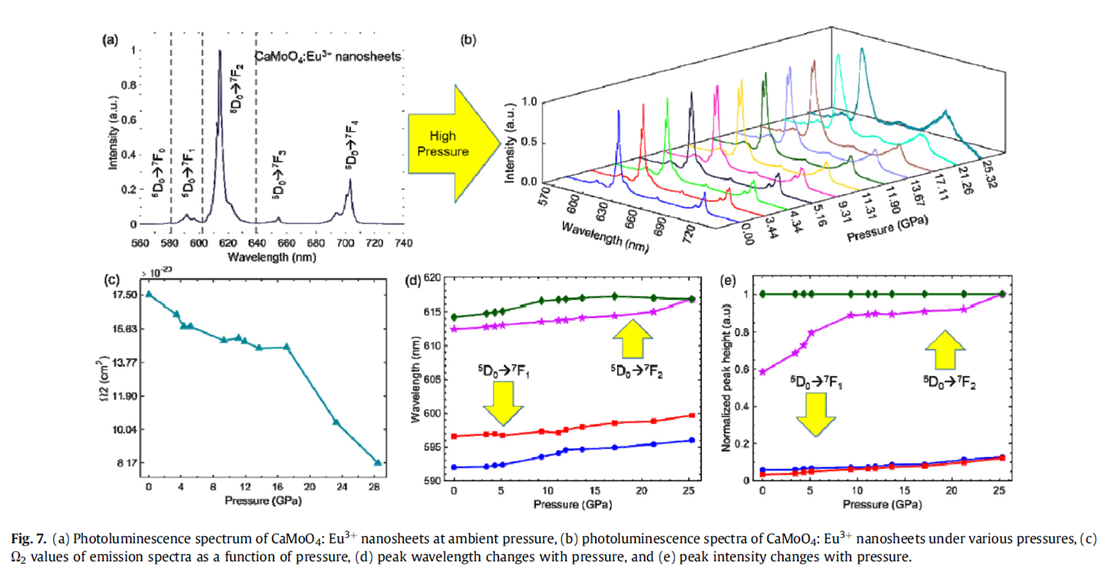
压强诱导结构相变