Reading 'Quantum and Dielectric Confinement Effects in Lower-Dimensional Hybrid Perovskite Semiconductors'
Quantum and Dielectric Confinement Effects in Lower-Dimensional Hybrid Perovskite Semiconductors
Introduction
perovskite network(sub-network): maintain some component of corner-sharing metal halide octahedra
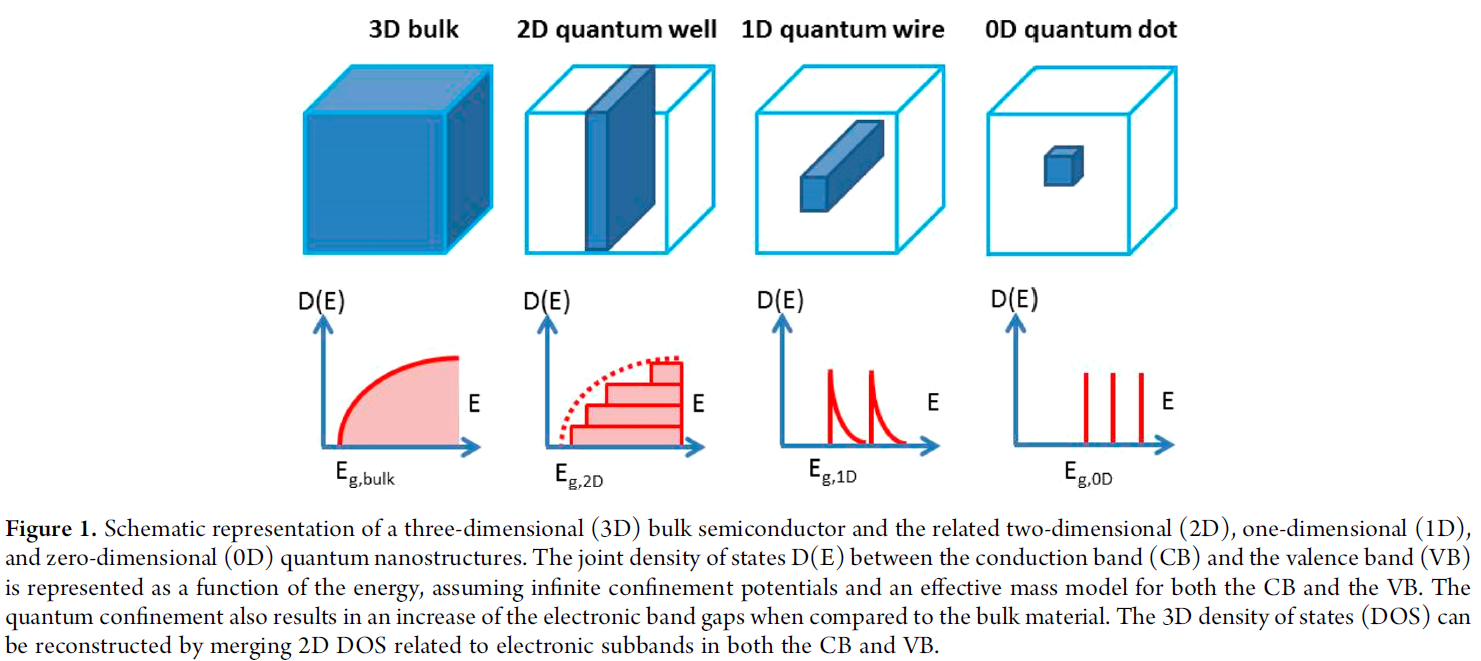
joint density of states(JDOS):
measures of the number of allowed optical transitions between the occupied valence band electronic states and the unoccupied conduction band electronic states separated by photon energy
低维材料的量子限域效应通常导致两个现象: - 受限方向上能级离散化(Quantum Well) - 维度降低,电子带隙增大
electronic dimensionality
describes the connectivity(overlap) of the atomic orbitals that comprise the lower conduction band(LCB) and the upper valence band(UVB). High electronic dimensionality is preferred for high-performance photovoltaic materials, because low electronic dimensionality leads to large effective mass of charge carrier.
CHEMICAL AND STRUCTURAL VIEWPOINT
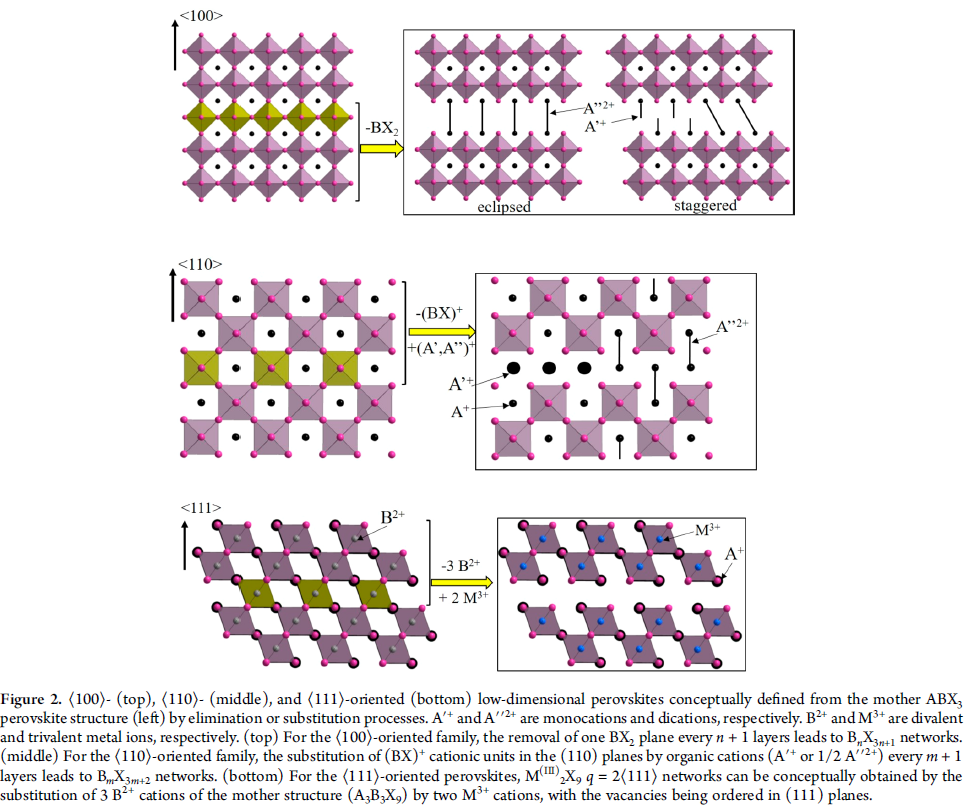
Perovskite Networks
⟨100⟩, ⟨110⟩, and ⟨111⟩ Layered Perovskite Series
将三维结构沿不同方向切割,再将其中部分离子替换
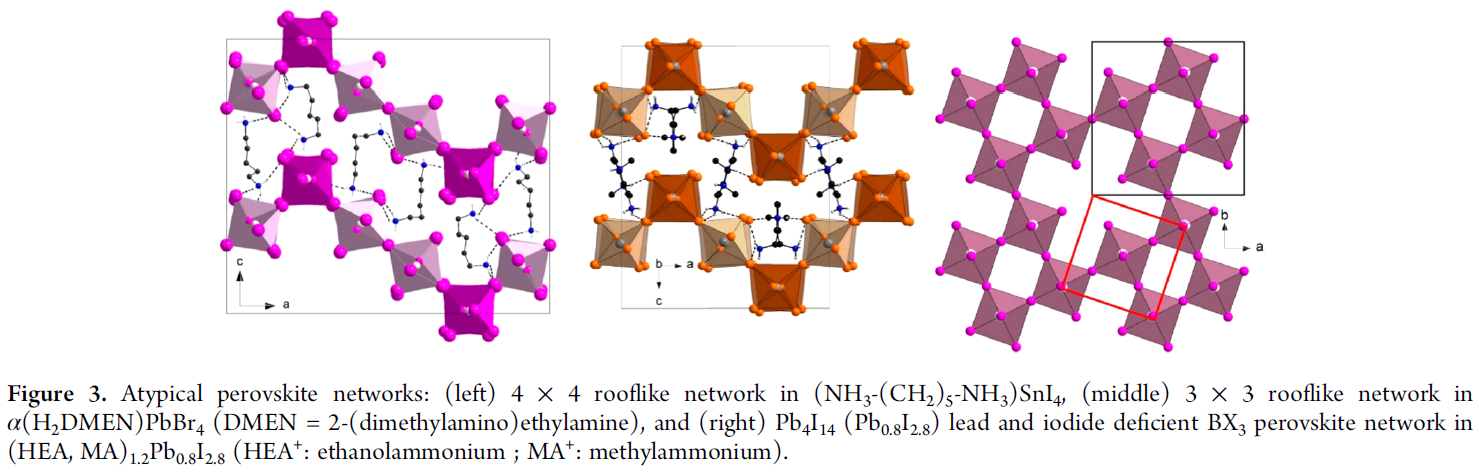
Atypical Perovskite Networks
“rooflike” networks 这类网络为同分异构体(与
有相同的分子式,但具有不同的结构,即其中四个卤族原子为corner-sharing,而其它两个为顶端原子),包含两种类型的八面体,一种是两个顶端原子在反式异构位置(同种配位体处于相反位置),另一种是两个顶端原子在顺式异构位置(同种配位体处于相邻位置)。表示为 rooflike褶皱层,其中n'和n"分别表示每半层roof的八面体数目 network 将 结构中每五个单位中的一个 单位替换为有机阳离子 ,从而产生 ( )
Halometallate Structures with Perovskite Subnetworks
钙钛矿网络属于金属盐网络的子网络,金属盐网路定义为包含corner-, edge-, or face-sharing
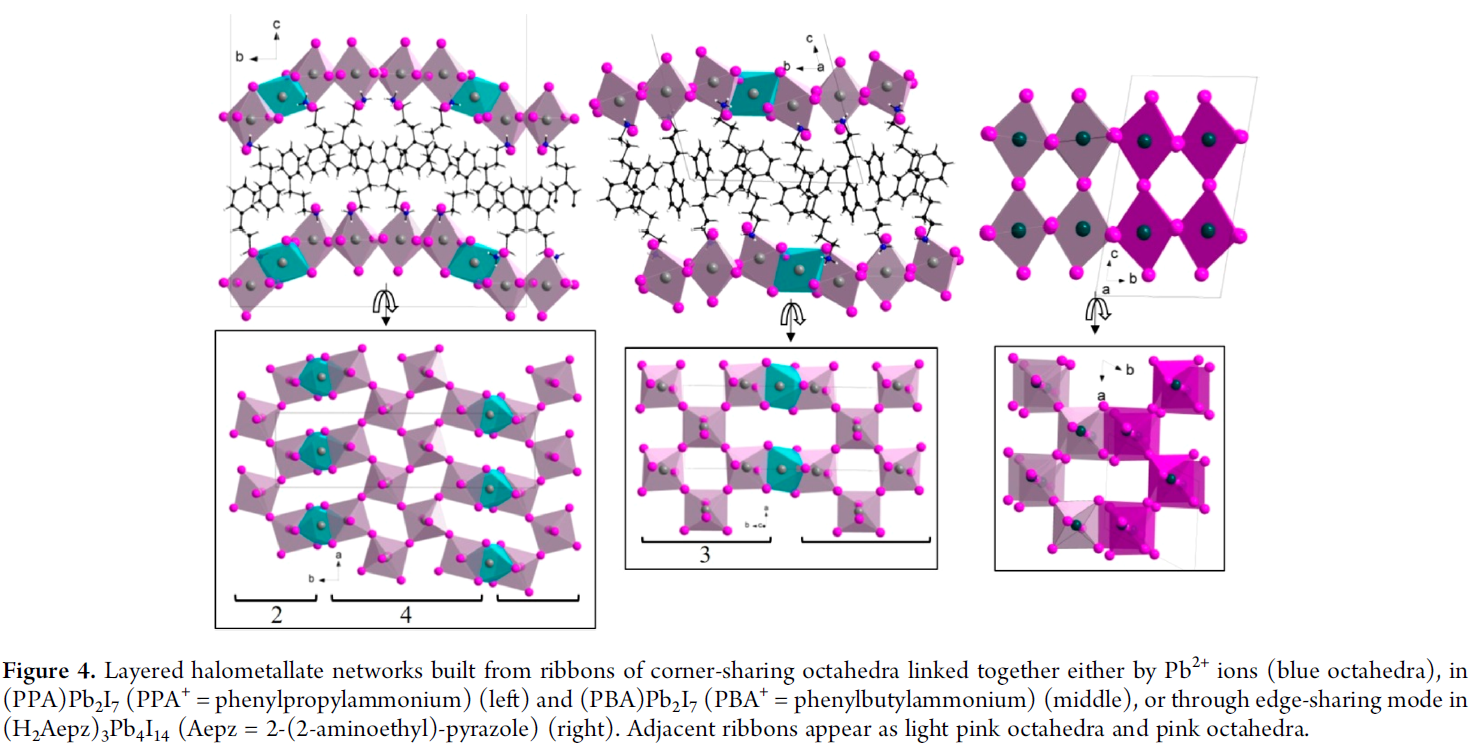
上图前两种为corner-和face-sharing八面体的组合网络,通常被描述为1D
上图第三种是corner-和edge-sharing八面体的组合网络。众所周知,对于<100>系列层状钙钛矿,带隙随着层数增加而减小,但是这种组合网络双层结构的带隙要比单层结构大。该现象可能的原因是量子限域效应表现在丝带的corner-sharing八面体中,意味着整体结构的电子维度要小于结构维度2D
Formation of Perovskite Networks/Choice of Organic Cations
⟨100⟩-Oriented Layered Perovskites
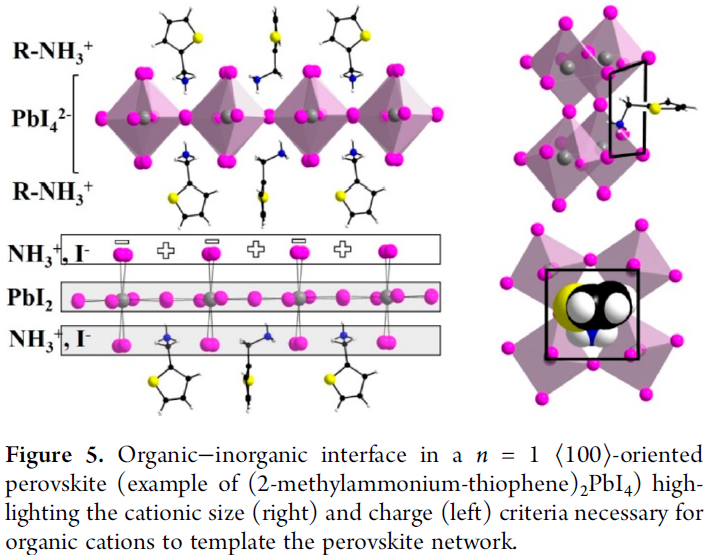
- 尺寸限制:阳离子宽度限制在阴离子组成的一个square-like格子中;对于有机阳离子的长度并没有严格的限制,因此相邻钙钛矿层之间的距离是可调控的
- 电荷限制:有机阳离子和卤族阴离子组成的中性层中间加着中性blocks
- distortion:越弱,带隙越小
- 八面体结构中
或 ns^2$ lone pair是stereoinactivity的,而非八面体结构中lone pair是stereoactivity,这一特性使钙钛矿材料容易形成self-trapped激子,利于输出白光 - in-plane and out-of-plane distortions
- 八面体结构中
- 极化率与电子和介电限域效应调控:
- 利用层间阳离子: 基于中性富电子共轭循环的有机阳离子更容易发生极化,因此可以弱化钙钛矿层的电子和介电限域效应
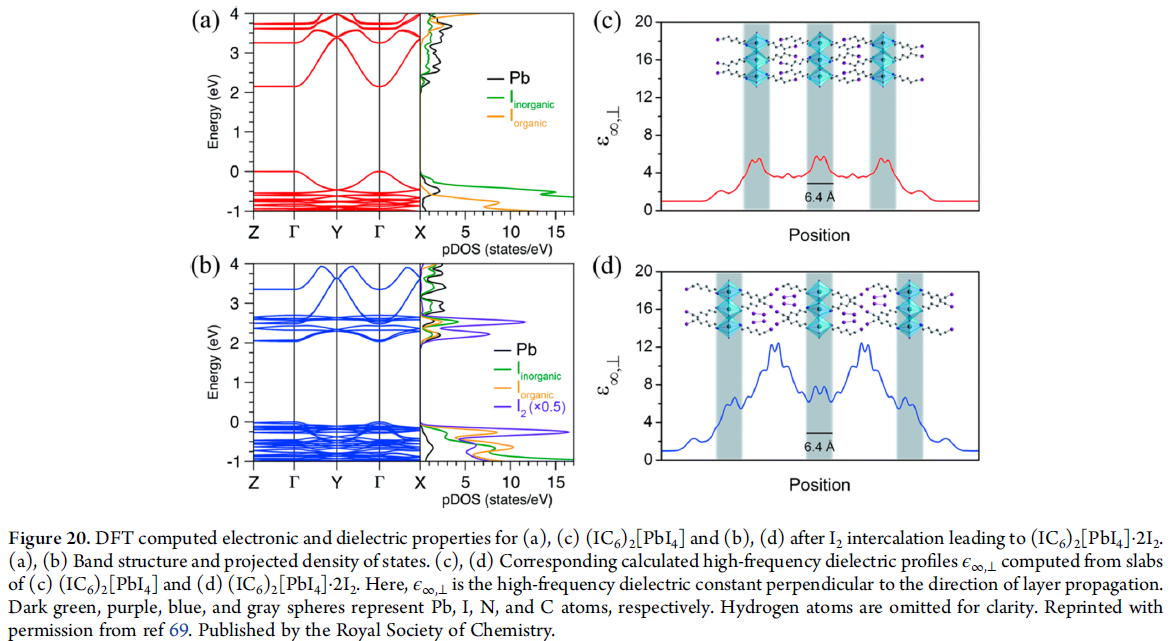
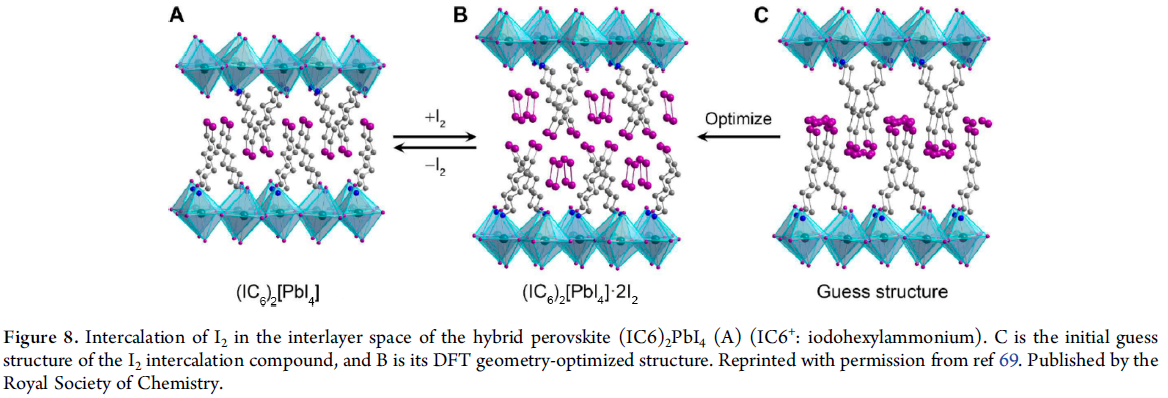
- 嵌入高度可极化分子:例如在有机层中嵌入碘分子,使得有机层介电常数增大,限域效应弱化
目前仅有m=2的<110>钙钛矿可以被结构表征。
Multilayered ⟨100⟩-Oriented Perovskites
Crystallographically Characterized Structures
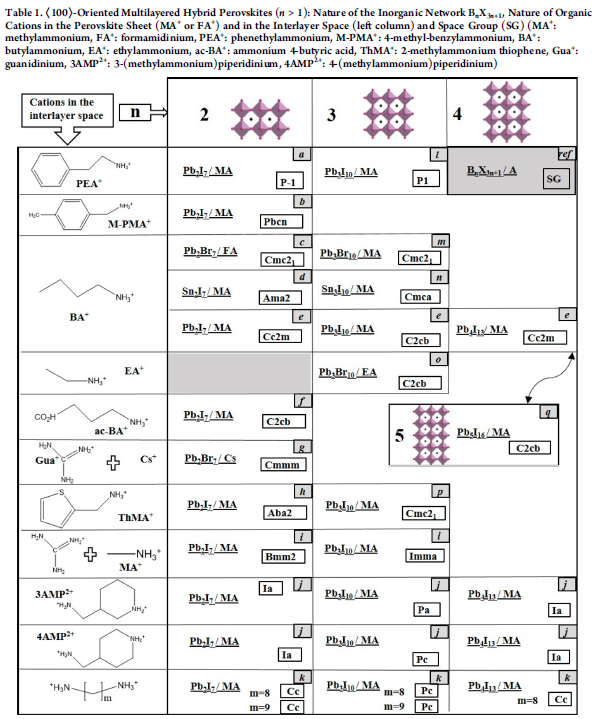
- 阳离子杂化结构:可能会提高电子维度,从而使能带色散程度更高
- 随着层数增加,层状钙钛矿更加趋向于稳定在非中心对称结构,进而表现出更显著的铁电效应
- 不同有机阳离子的层状钙钛矿表现出不同的in-plane和out-of-plane distortion,而且随着层数增加,distortion的程度变化也不同,可能增大,也可能减小
- 加入不同有机阳离子进行研究时,需要考虑多层钙钛矿,以及相应单层和3D情况的形成能
MULTILAYERED HALIDE PEROVSKITES: QUANTUM CONFINEMENT
Electronic Band Structure
- The HOMO-LUMO gap: 孤立原子最高占据和最低非占据分子轨道的能量差
- The DFT gap:基于KS DFT理论计算得到的最高占据价带和最低非占据导带电子态的能量差;不能解释移除和添加一个电子时的能量变化
- The transport or electrical or fundamental gap:等于离子化能(拿走一个电子的能量)和电子亲合势(添加一个电子的能量)之差;可通过能量差(
),或者时多体微扰理论(例如:GW近似)计算;实验上通过提供占据VB态信息的ultraviolet photoemission spectroscopy(UPS)和提供非占据CB态信息的inverse photoemission spectroscopy (IPES)得到 - The optical band gap energy:实验上通过光致发光谱(PL)或者观察光吸收谱得到。其值等于材料本征带隙减去激子束缚能;对于直接带隙半导体,本征带隙对应于fundamental gap
Brief Overview of Theoretical Approaches and Relation to Experiments
- GW:自洽GW或者简化的GW修正方法(
)可以更精确地近似得到fundamental gap; - Bethe−Salpeter Equation (BSE):描述两体相对论系统的束缚态,可以解释激子效应
- TDDFT:激发态性质(光学性质),可以包含非绝热分子动力学(NAMD)
Ways to Handle the Organic Cations
- 有机阳离子在近室温下无序,不满足site symmetry,可以通过补偿背景电荷密度或者替代有机阳离子为碱金属进行DFT计算
- 当介电限域效应作用时,由于有机阳离子的介电常数通常小于无机层,因此不能轻易做替换,则上述近似不再有用;
- DFT结构优化得到的结构均为零温基态结构
- 对于低能态和高能态,清晰地描述有机阳离子是必要的
- 有机阳离子具有很明显的动力学性质(动力学无序和势能耗散)
- $
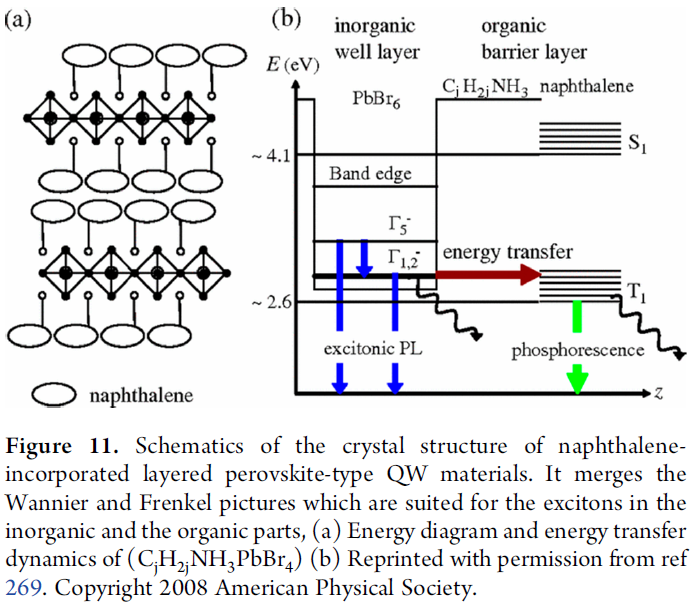
Electronic Band Edge States.
- 成键类型可以通过电子波函数图看出来:成键波函数无节点,反键波函数存在节点
- SOC对band diagram的影响(Rashba or Dresselhaus effects:空间反演破缺,保有时间反演对称性)
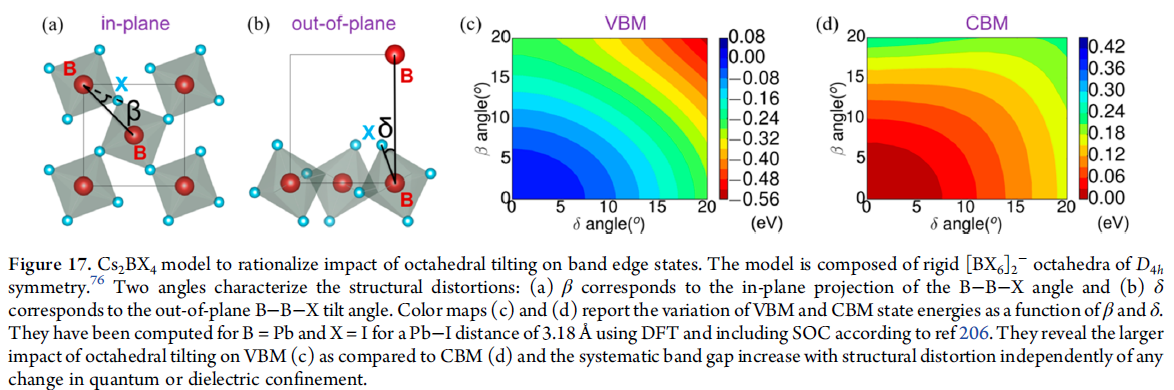
- structural distortions(e.g. octahedral tilting)对band diagram的影响;同时影响电子和空穴局域在钙钛矿层;DFT结构优化会影响distortion程度,进而影响带隙计算
- 将有机分子替换为碱金属阳离子来查看电子密度局域化是否与有机阳离子特定偶极取向相关
Effective Masses from Band Structures
DFT计算的有效质量乘以实验和DFT带隙之比可以得到更接近实验的有效质量
Concept of Quantum Confinement Applied to Multilayered Halide Perovskites
传统的3D Bloch波函数暗示在stack轴向上,电子是退局域化的;另一个观点采用了2D的Bloch波函数表示,使得out-of-plane的周期性破缺,导致stack轴向上允许电荷局域化,即由于超晶格(两种材料按照一定周期性交替生长)效应形成量子阱,在一维方向上限制载流子运动,从而导致热力学或者缺陷诱导的能量耗散;较强的电声耦合相互作用也能引起电荷局域化。为了用DFT研究stack轴向上的电子态局域化,需要非常大的超胞计算,并考虑局域晶格distortion,缺陷以及分子动力学
fluctuations
当能量中某些部分并不以期待的形式输出时,即为耗散 - thermal:能量以热能形式耗散 - defect-induced:载流子被缺陷态捕获,发生非辐射复合
需要依据单层和3D钙钛矿电子结构之间的关系来理解上述两种效应的作用,并研究如何通过2D DOS来重新构造3D-like DOS
目前仍需要多层钙钛矿完整的对称性分析(可判断是否可以跃迁,能级兼并和分裂情况)
禁带跃迁
- 宇称为偶的算符(角动量算符)连接宇称相同的态
- 宇称为奇的算符(位置和动量算符)连接宇称相反的态
能带对齐
band alignment计算的关键在于参考能级的选取(真空能级,core电子能级或者其它方法)
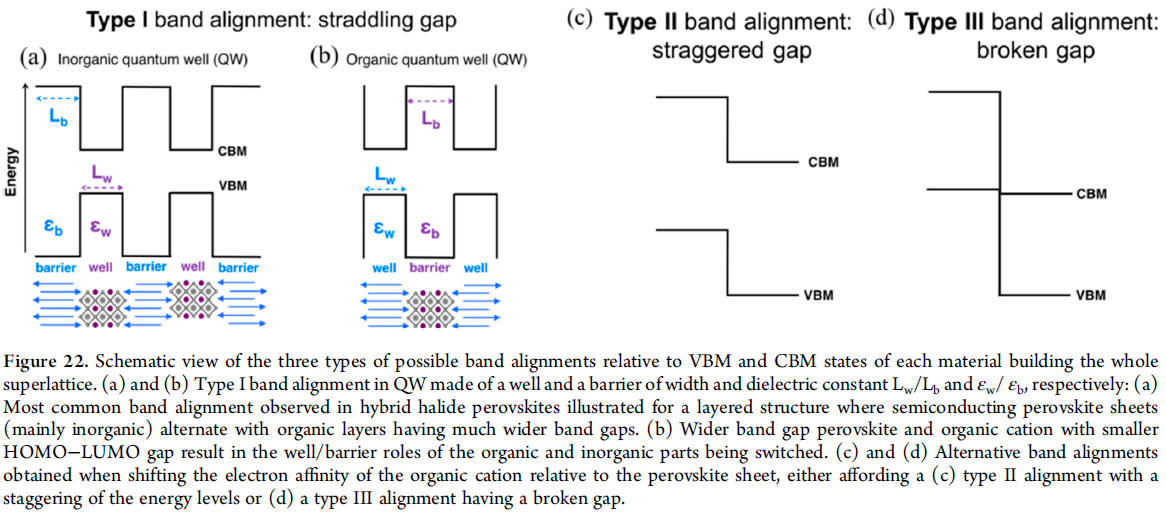
Type-1 QW 中电子和空穴将限制在well内,使得辐射复合提高,而且导致比3D材料更高的激子束缚能;大多数层状卤化物钙钛矿均采用该种结构,除了部分有机层采用短链有机分子的情况
MULTILAYERED HALIDE PEROVSKITES: DIELECTRIC CONFINEMENT
Excitons
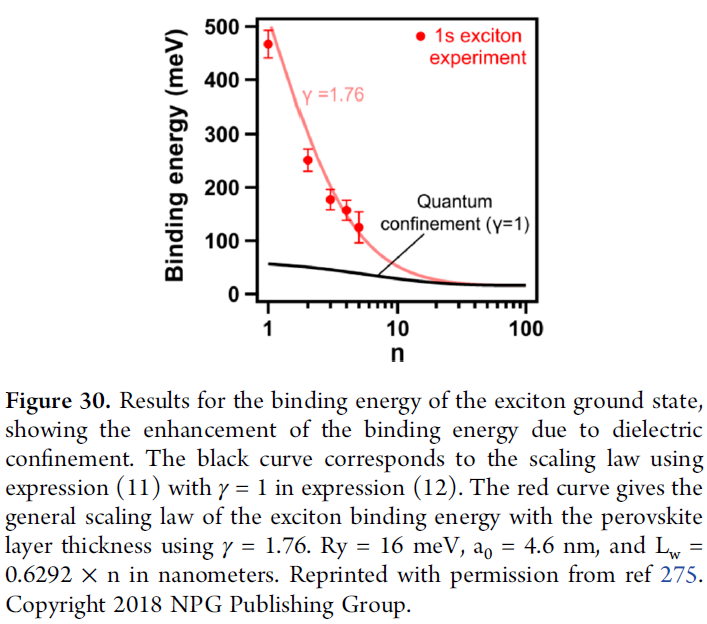
层状钙钛矿的激子束缚能通常较小,因此激子为Wannier激子,可以采用2D类氢模型近似描述
Single Particle Self-Energies and Electron−Hole Pair Interactions-Shortcomings of Simplified Descriptions for Layered Perovskites
- Wannier-Mott类氢模型并不能很好的捕获介电限域效应的影响,以及描述能量随QW厚度的响应
- 用点电荷描述电子-空穴相互作用,会造成相应自能描述的不一致性,具体而言就是自能积分发散
- 由于层状钙钛矿的介电不均匀,所以并不能用单一介电常数表示介质极化率
self-energy
自能:即单粒子从无穷远处拉到特定构型中所需要的能量,也就是粒子与系统相互作用后所拥有的能量
Many-Body Approaches to the Single Particle Self-Energies and Electron−Hole Interaction
- 层状钙钛矿计算的关键问题在于合理地评估两点介电函数(对于GW而言,虽然考虑了自能贡献,但是对于大体系地计算要求非常高)
解BSE方程可以得到激子能量和波函数 1. DFT+GW计算 - 先通过GW计算得到VB和CB态波函数 - 再基于DFT计算得到的VB和CB能量,以及GW得到的屏蔽库仑相互作用W构建有效哈密顿量,对角化得到exciton envelope function - 最后求和构建激子波函数
- 求解Bloch方程
- 单条能带哈密顿量的经验有效质量近似(或者多条能带经验哈密顿量的k.p近似)得到单粒子能量和波函数;
- 构建有效哈密顿量(需要额外提供合适的屏蔽相互作用W描述)得到exciton envelope function
- 从一个Dyson-like的方程迭代求解激子格林函数
具体计算公式可见NC文章
局域性
作用势表达式中的相对距离表示
若位势还与角动量等其它量相关的话,则为非局域势(例如赝势的非局域部分)
Image Charges and Dielectric Confinement
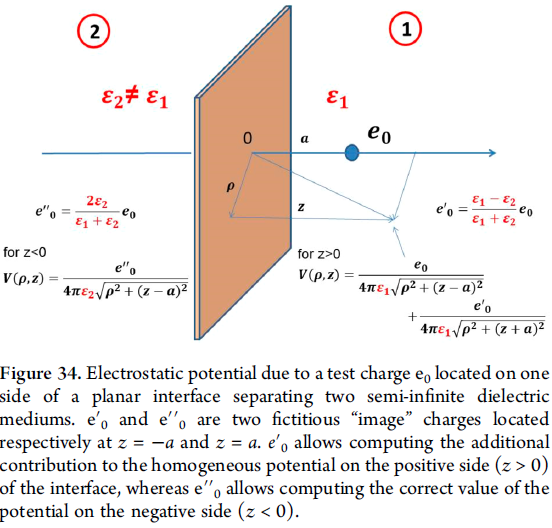
由于平板界面两侧假想电荷不等价,所以静电势时非局域的。
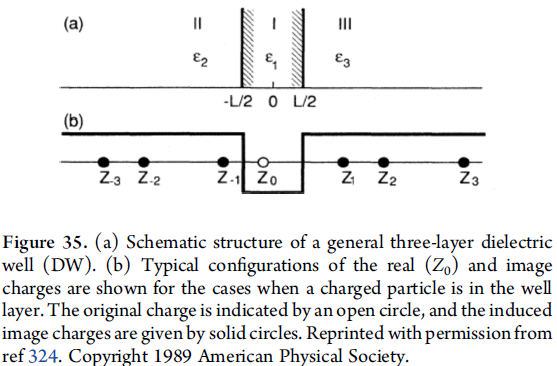
- dielectric well(DW) with abrupt interfaces:barrier为半无限大的介质
- dielectric superlattices(DSL):在DW基础上还要考虑barrier的厚度,层状钙钛矿可采用该模型
假想电荷模型用于评估自能贡献
- 介电不均匀导致的自能修正:
- 为解决额外界面处自能修正的数值收敛问题,通常采用移动界面或者假定电子态完全受限于势阱
- 由于无机层stacking轴方向上的介电常数和面内介电常数是不一致的,而且有机层本身也是各向异性的,因此平均介电常数仅适用于面内(
),stacking轴方向上的平均介电常数对提高激子束缚能有影响( )。 当且仅当 时,即bulk无机层对应于3D cubic相钙钛矿时出现
- 解决abrupt interfaces处问题的更一般方法:
a partial Fourier transform of the inhomogeneous Poisson equation with a test charge
at : DW with abrupt interface 的电子-空穴相互作用
其中
- barrier层的有效质量是非常大的